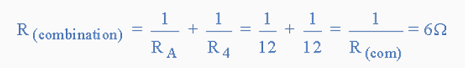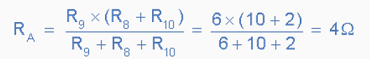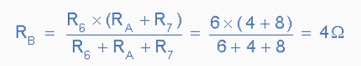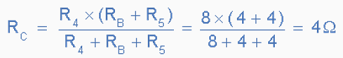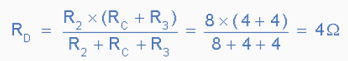|
In the previous two tutorials we have learnt how to connect resistors together to form either a Series Circuit or a Parallel Circuit and used Ohms Law to find the circuit currents and voltages. But what if we want to connect resistors together in "BOTH" parallel and series combinations within the same circuit to produce more complex circuits that use resistor combinations, how do we calculate the combined circuit resistance, currents and voltages for this. |
||
|
Resistor circuits that combine series and parallel resistors circuits together are generally known as Resistor Combination or mixed circuits and the method of calculating their equivalent resistance is the same as that for any individual series or parallel circuit and hopefully we now know that resistors in series carry exactly the same current and that resistors in parallel have exactly the same voltage across them. |
||
|
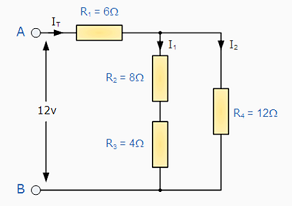
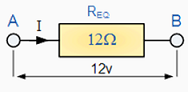
For example, Calculate the total current ( I ) taken from the 12v supply. |
||
|
|
||
|
At first glance this may seem a difficult task, but if we look a little closer we can see that the two resistors, R2 and R3 are both connected together in a "SERIES" combination so we can add them together. The resultant resistance for this combination would therefore be, |
||
|
R2 + R3 = 8 Ω + 4 Ω = 12 Ω |
||
|
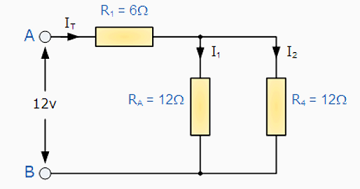
So now we can replace both the resistors R2 and R3 with a single resistor of resistance value 12 Ω |
||
|
|
||
|
Now we have single resistor RA in "PARALLEL" with the resistor R4, (resistors in parallel) and again we can reduce this combination to a single resistor value of R(combination) using the formula for two parallel connected resistors as follows. |
||
|
|
||
|
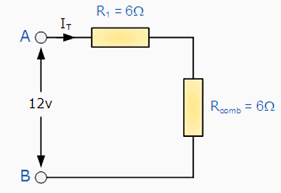
The resultant circuit now looks something like this: |
||
|
|
||
|
The two remaining resistances, R1 and R(comb) are connected together in a "SERIES" combination and again they can be added together so the total circuit resistance between points A and B is therefore given as: |
||
|
R( A - B ) = Rcomb + R1 = 6 Ω + 6 Ω = 12 Ω. |
||
and a single resistance of just 12 Ω can be used to replace the original 4 resistor combinations circuit above. Now by using Ohm´s Law, the value of the circuit current ( I ) is simply calculated as: |
||
|
|
||
|
So any complicated circuit consisting of several resistors can be reduced to a simple circuit with only one equivalent resistor by replacing the resistors in series or in parallel using the steps above. It is sometimes easier with complex resistor combinations to sketch or redraw the new circuit after these changes have been made as a visual aid to the maths. Then continue to replace any series or parallel combinations until one equivalent resistance is found. Lets try another more complex resistor combination circuit. |
||
|
|
||
Example No2 |
||
|
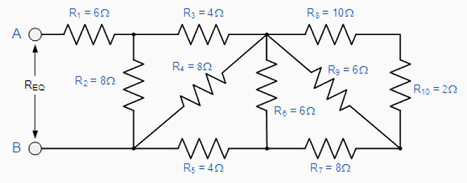
Find the equivalent resistance, REQ for the following resistor combination circuit. |
||
|
|
||
|
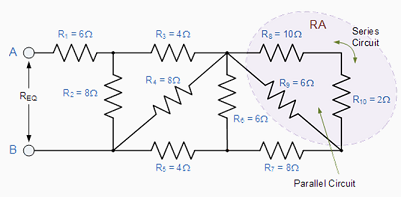
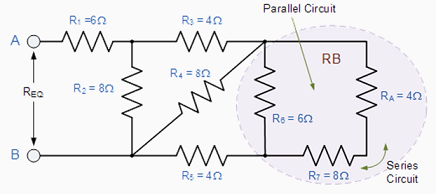
Again, at first glance this resistor ladder circuit may seem complicated but as before it is a combination of series and parallel resistors connected together. Starting from the right hand side and using the simplified equation for two parallel resistors, we can find the equivalent resistance of the R8 to R10 combination and call it RA. |
||
|
|
||
|
|
||
|
RA is in series with R7 therefore the total resistance will be RA + R7 = 4 + 8 = 12Ω as shown. |
||
|
|
||
|
This resistive value of 12Ω is now in parallel with R6 and can be calculated as RB. |
||
|
|
||
|
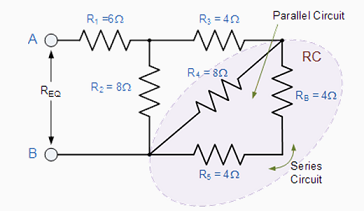
RB is in series with R5 therefore the total resistance will be RB + R5 = 4 + 4 = 8Ω as shown. |
||
|
|
||
|
This resistive value of 8Ω is now in parallel with R4 and can be calculated as RC as shown. |
||
|
|
||
|
RC is in series with R3 therefore the total resistance will be RC + R3 = 8Ω as shown. |
||
|
|
||
|
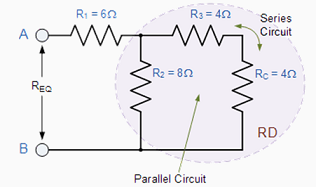
This resistive value of 8Ω is now in parallel with R2 from which we can calculated RD as. |
||
|
|
||
|
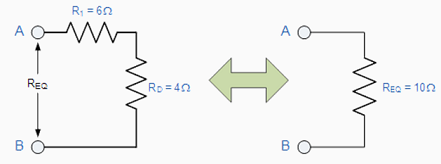
RD is in series with R1 therefore the total resistance will be RD + R1 = 4 + 6 = 10Ω as shown. |
||
|
|
||
|
Then the complex combination resistive network above can be replaced with one single resistance of value 10Ω. |
||
|
In any Series-Parallel Resistor Combination circuit by firstly identifying simple series or parallel connected resistors and replacing them with individual resistors of the equivalent value, it is easily possible to reduce any complex circuit to that of a single equivalent resistance. However, calculations of complex Bridge and T networks which cannot be reduced to a simple parallel or series circuit using equivalent resistances need to be solved using Kirchoff's Current Law, and Kirchoff's Voltage Law which will be dealt with in another tutorial. |
||
|
In the next tutorial about Resistors, we will look at the electrical potential difference (voltage) across two points including a resistor. |
||
|
|
||
| Reproduced with permission from Wayne Storr ( http://www.electronics-tutorials.ws/resistor/res_5.html ) |
||